Linear equations are equations having variables with power 1. ax+b = 0 is an example with one variable where x is the variable, a and b are real numbers. In this article we learn the definition, type of solutions, how to solve these equations with one variable and two variables using different methods along with examples.
Linear algebra is a subject of great breadth. Its spectrum ranges from the abstract through numerical techniques to applications. Linear algebra is used in many various fields such as fractal geometry, differential equations, difference equations, relativity, archaeology, demography and many more. In daily life, we come across various situations where we need to frame the problems into equations to solve them.
What is Linear Equation in Maths?
The statements of equality of two mathematical expressions involving one or more variables is known as equation. An equation in which the highest power of the variable is one is known as linear equation.
Mathematically: An algebraic equation that can be written in the form ax + b = 0 or ax + by + c = 0, where a, b and c are real numbers and x and y are variables with the highest power one.
Standard Form of a Linear Equation
Consider a, b, c, a1 , a2 , b1 , b2 and d are real numbers and x, y, z are variables.
| Terms | Definition | Standard Form | Example |
| Linear Equations in One Variable | An equation has only one variable. | ax + b = 0 | 2x – 3 = 0 |
| Linear Equation in two Variables | An equation has only two variables. | ax + by + c = 0 | 3x + 7y + 4 = 0 |
| Linear Equation in Three Variables | An equation has three variables. | ax + by + cz + d = 0 | x + 7y + 4z -1 = 0 |
| Linear Equations with Fractions | Equation containing fractional terms. | x/a = c | 2x/3 = 4 |
| Slope Intercept Form | Equation in the form: y = mx + c. | y = mx + c, where ‘m’ = slope and ‘c’ = y-intercept | y = 3x + 10 |
| Point Slope Form | Equation passing through a point (x1, y1). | y − y1 = m(x − x1) where m = slope | y – 3 = 10(x – 5);
Line passing through point (3, 5) |
| Pair of linear equations in two variables | Set of two or more linear equations containing same number of variables | Pair of 2 equations:
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 |
3x + 4y = 4 and
5x + 7y = 3 |
In general:
A general system of m linear equations with n unknowns:a11x1 + a12x2 + ….+ a1nxn = b1
a21x1 + a22x2 + ….+ a2nxn = b2
.
.
.
am1x1+am2x2+….+amnxn = bm
Where x1, x2, x3,…..,xn variables and b1, b2,…., bm constant terms and a11, a12,…….,amn coefficients of any system of linear equations.
Solution of Linear Equations
Linear equations can be used to solve any arithmetic equations and determine the exact value/root of the variable which satisfies the equation.
Solving Linear equation in one variable
The basic principle used in solving any linear equation is that any operation performed on one side of the equation must also be performed on the other side of the equation. Following are important rules to solve linear equations:
- Additional rule
- Subtraction rule
- Multiplication rule
- Division rule
Solving Systems of Linear Equations
How to solve linear equations in two variables? Linear Equations of two variables can be solved by different methods as listed below. For the equations involving two variables, we need two equations having the same variables to find the roots.
Methods to solve:
- Method of substitution
- Cross multiplication method
- Method of elimination
- Matrix method
- Determinant methods
Before we start solving linear equations having two variables, advised checking the type of solution, whether consistent or inconsistent. Follow the below chart to check the same.
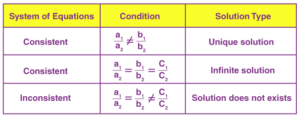
Linear Equations and Inequalities
A statement involving one or more variables having degree one is called a linear equation whereas inequalities connect the algebraic expressions by inequality signs (greater than (>), less than (<), greater than equal to (≥), and less than equal to (⩽).
Solved Problems on Linear Equations
Example 1: Solve 3x – 5 = 10 and check the answer.
Solution: 3x – 5 = 10
Transposing -5 to RHS,
3x = 10 + 5
3x = 15
Divide each side by 3, we get
3x/3 = 15/3
x = 5
Checking:
Substituting x = 5 in the given equation.
3(5) – 5 = 10
15 – 5 = 10
10 = 10
Result is true.
Example 2: Solve (3x + 4)/(x – 6) = 2/3
Solution: (3x + 4)/(x – 6) = 2/3
Using cross-multiplication, we get
3(3x + 4) = 2(x – 6)
9x + 12 = 2x – 12
7x = -24
or x = -24/7
Example 3: Solve Simultaneous Linear Equations by substitution method
2x + 3y = 25 and 3x + 2y =25
Solution:
2x + 3y = 25 …(i)
3x + 2y =25 ….(ii)
Isolate equation (i) for x
x = (25 – 3y)/2
Substituting the value of x in (ii)
3((25 – 3y)/2) + 2y = 25
(75 – 9y)/2 + 2y = 25
75 – 9y + 4y = 50
– 5y = -25
or y = 5
Now, find the value of x
(i)=> 2x + 3(5) = 25
x = 5
Therefore, x = 5 and y = 5 is the solution set.
Linear Equations Word Problems
One helpful approach when solving any algebraic word problem is to translate the word problem into an equation then solve the equation. Let us solve some of the problems to understand the concept.
Problem 1: Ten years ago, Sudheer was twelve times as old as Arshad and ten years hence, he will be twice as old as Arshad will be. Find their present ages.
Solution:
Consider Sudheer’s present age is x years and Arshad is y years older.
As per the given data,
| Arshad’s Age | Sudheer’s Age | Equation | |
| Present Age | y | x | |
| 10 years ago | y – 10 | x – 10 | x – 10 = 12(y – 10) |
| 10 years hence | y + 10 | x + 10 | x + 10 = 2(y + 10) |
We have two equations:
x – 10 = 12(y – 10) and
x + 10 = 2(y + 10)
Solving the above equations and finding the values of x and y.
x – 12y = -110 ….(i)
and
x – 2y = 10 or x = 10 + 2y …(ii)
Substituting the value of x in (i)
(10 + 2y) – 12y = -110
10 – 10y = -110
or y = 12
Now, (ii) implies
x = 10 + 2(12)
or x = 34
Therefore, Sudheer is 34 years old and Arshad is 12 years old.
Problem 2: Raksha’s mother asked her to buy one candy and three pencil for Rs. 10. Again, she was asked to buy two candies and one pencil for Rs. 5 of the same kind. Find the cost of one candy and one pencil.[Apply cross multiplication Method]
Solution:
Let x be the cost of one pencil and y be the cost of one candy.
One candy and three pencil for Rs. 10 => 3x + y = 10
Two candies and one pencil for Rs. 5 => x + 2y = 5
Method for cross multiplication:
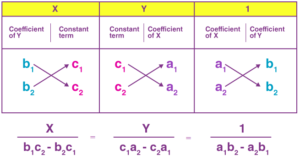
Using the above formula, we have
a1 = 3, b1 = 1, c1 = -10
a2 = 1, b2 = 2, c2 = -5
=> x = 15/3 = 3
and y = 5/5 = 1
The cost of one pencil is Rs. 3 and the cost of one candy are Rs. 1.
Problem 3: The shaded region shown in the figure is given by the equations
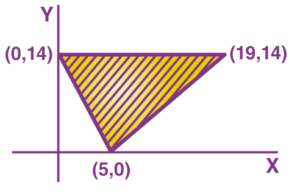
Solution:
From the figure, it is clear that there are 3 lines.
The line which passes from (0, 14) and (19, 14) is y = 14.
∴ In the shaded region 0 ≤ y ≤ 14.
Line which passes from (5, 0) and (0, 14) is 14x + 5y = 70.
∴ In the shaded region 14x + 5y ≥ 70.
The line which passes from (5, 0) and (19, 14) is x − y − 5 = 0
∴ In the shaded region x − y ≤ 5.
Thus, inequations are 14x + 5y ≥ 70, x − y ≤ 5, y ≤ 14.
Problem 4: The number of real values of parameter k for which
will have exactly one solution is
Solution:
The equation is
.
put y = log16 x
then y2 – y + log16 k = 0
for exactly one solution b2-4ac = 0
1 – 4 log16 k = 0
log16 k = 1/4
k = 161/4
= 2
Problem 5: The solution set of the inequality 37 − (3x + 5) ≥ 9x − 8 (x − 3) is
Solution:
We have, 37 − (3x + 5) ≥ 9x − 8 (x − 3)
(37 − 3x − 5) ≥ 9x − 8x + 24
⇒ 32 − 3x ≥ x + 24
Transferring the term 24 to L.H.S. and the term (−3x) to R.H.S.
32 − 24 ≥ x + 3 x ⇒ 8 ≥ 4x
⇒ 4x ≤ 8
Dividing both sides by 4.
4x / 4 ≤ 8 / 4
⇒ x ≤ 2
∴ Solution set is (−∞, 2].
Problem 6: The solution set of (x)2 + (x + 1)2 = 25, where (x) is the least integer greater than or equal to x, is
Solution:






